In matematica, il quadrato magico è una serie di numeri distinti disposti a forma di quadrato in modo che la somma di ogni riga, di ogni colonna e di ogni diagonale principale sia uguale. Ad esempio un quadrato magico di ordine 3 (l'ordine rappresenta il numero di righe orizzontali o di colonne verticali), ha somma costante è 15:

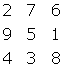
Nell'antichità queste configurazioni erano ritenute magiche e considerate al pari di amuleti o portafortuna; solo in un secondo tempo divennero oggetto di studio dei matematici.
I numeri contenuti in un quadrato magico di ordine n sono quasi sempre gli interi 1, 2, 3, ..., n². Poiché la somma dei primi n² interi 1, 2, 3, ..., n² è:

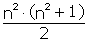
la somma di ciascuna delle n righe, delle n colonne, o delle diagonali principali del quadrato magico è data da:

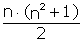
e questo numero prende il nome di costante del quadrato magico.
Oltre alle diagonali principali, che nel caso del quadrato di ordine 3 sono le terne (2, 5, 8) e (6, 5, 4), si possono considerare anche le diagonali spezzate, vale a dire (7, 1, 4), (6, 9, 3), (2, 1, 3) e (7, 9, 8). Così, un quadrato magico si dice panmagico o pandiagonale se anche la somma di ogni diagonale spezzata è uguale alla costante del quadrato magico. Il quadrato magico di ordine 3 mostrato sopra non è panmagico, mentre quello di ordine 4 è panmagico di costante 34.

Un quadrato magico si dice bimagico, o doppiamente magico, se rimane magico anche dopo aver sostituito i suoi elementi con i rispettivi quadrati; analogamente si dice trimagico se rimane magico dopo averne sostituito gli elementi con i rispettivi cubi.
In generale, un quadrato magico di elementi 1, 2, ..., n² esiste per ogni ordine n eccetto per n = 2. Non è ancora stata scoperta, tuttavia, alcuna regola universale valida per costruire tutti i quadrati magici, e non è chiaro quale sia il numero di quadrati magici distinti per ogni ordine n. Per ora sono state studiate tre classi diverse di regole per la costruzione di quadrati magici particolari: quelle per gli n dispari, quelle per gli n divisibili per 2 ma non per 4, e quelle per gli n divisibili per 4. Sono state costruite inoltre altre figure geometriche magiche, tra cui i cubi magici.

Il quadrato latino è un tipo di quadrato magico che ha per elementi gli interi 1, 2, ..., n (o qualunque altro gruppo di n numeri distinti), ciascuno dei quali ripetuto n volte, disposti in modo che gli interi di ogni fila e di ogni colonna siano tutti distinti. Esempi di quadrati latini sono:

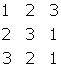  e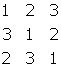  

Se si sovrappone il secondo sul primo, mantenendo lo stesso ordine di ciascuno, si ottiene il quadrato di coppie seguente in cui nessuna coppia si ripete:

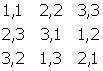
Un quadrato di coppie senza ripetizioni, come quello precedente, si chiama quadrato di Eulero, dal nome del matematico svizzero Leonhard Euler, o quadrato greco-latino.